A 90 percent confidence limit is a range of values that is likely to contain the true population value with a probability of 90%. It is calculated using the sample mean and standard deviation, along with the size of the sample. The 90% confidence interval can be determined by adding and subtracting 1.645 times the standard error from the sample mean.
This provides an upper and lower bound for which we are confident contains our true population value within its bounds around 90% of the time.
When conducting statistical tests, the 90 percent confidence limit is used to measure a dataset’s reliability. This confidence level indicates that there is a 90% probability that the true value of a parameter lies within certain limits derived from the sample data. The higher the confidence limit, the more reliable and accurate our results are likely to be.
With this in mind, it’s important to strive for high levels of accuracy when interpreting data by utilizing an appropriate confidence level.
90% Confidence Limit
Is 90% Confidence Level Acceptable to Research?
Yes, 90% confidence level is generally accepted as an acceptable level of confidence in research. This means that if a researcher conducted the same study repeatedly, they would expect to get similar results at least 90% of the time. Generally speaking, a higher level of confidence (95 or 99%) is preferred for more important decisions and studies with larger sample sizes.
However, for smaller studies or quick decision-making processes where large sample sizes are not feasible, 90% can be considered satisfactory due to its balance between accuracy and practicality.
Is an 80% Confidence Interval Wider Than 90%?
Yes, an 80% confidence interval is wider than 90%. This is because a higher level of confidence requires more data points to be included in the interval. The larger the sample size and degree of confidence, the narrower the range of probability will be for any given statistic.
To illustrate this further, let’s consider a hypothetical example: if we were looking at polling data for an upcoming election and wanted to calculate a 90% confidence interval, we would need to include more survey respondents in our sample size (and thus have greater accuracy) than if we were calculating an 80% confidence interval.
Credit: www.numerade.com
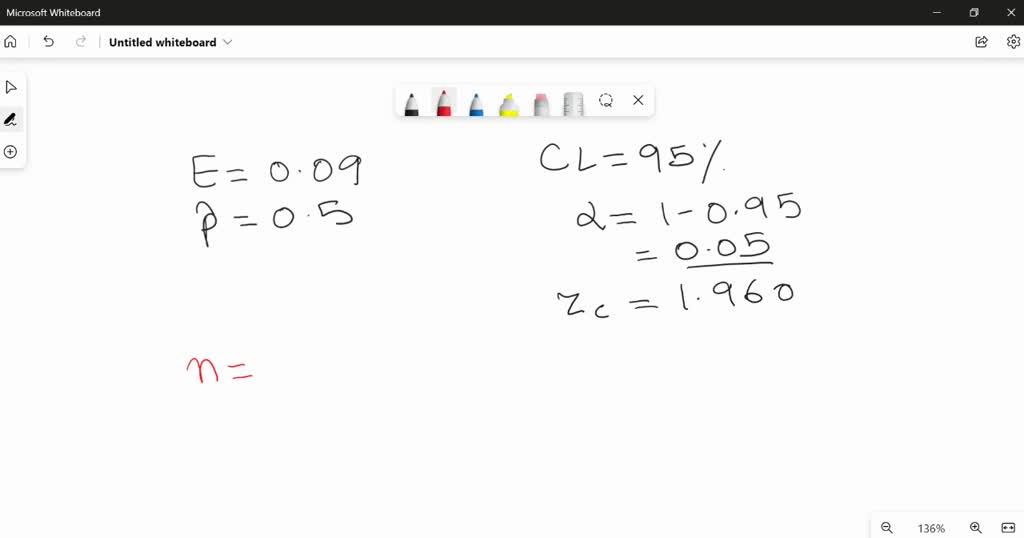
90 Percent Confidence Limit Formula
The 90 Percent Confidence Limit Formula is a mathematical equation used to calculate the lower and upper confidence limits for an estimated population proportion. The formula requires knowledge of the sample size, mean and standard deviation in order to accurately calculate these limits. Knowing the confidence interval can help researchers draw conclusions about their data set with greater certainty.
90 Percent Confidence Limit Calculator
A 90 Percent Confidence Limit Calculator is a powerful tool that can be used to calculate the confidence interval for a population mean with a given sample size. This calculator provides an easy-to-use interface, allowing users to input their data and get accurate results in seconds. The result of this calculation will tell you the probability that your population mean falls within a certain range.
Knowing this information can help you make more informed decisions when analyzing data and making predictions about future trends.
90 Percent Confidence Interval Z-Score
A 90% confidence interval z-score is a score that indicates the probability of an observed result falling within a range of values. This can be used to assess whether the results of a study are statistically significant, and it is often calculated using standard deviation and sample size. The higher the z-score, the more confident we can be that our results are accurate.
Conclusion
This blog post illustrated the importance of understanding the concept of 90% confidence limits. Not only is it helpful to know what this means statistically, but also how its application can be used in a variety of ways such as interpreting research results or data analyses. Additionally, it was shown that when calculating the 90% confidence limit, one must take into account both sample size and variability.
With this knowledge, one can have an increased level of accuracy in their analysis and use more reliable methods for presenting data.